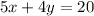Answer:
Part 1)
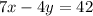
Part 2)
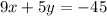
Part 3)

part 4)
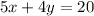
Explanation:
we know that
The standard form of the equation of the line is equal to

where
A is a positive integer
B, and C are integers
Part 1) Determine the standard form of the equation of the line that passes through
 and
and

we know that
The formula to calculate the slope between two points is equal to

Substitute the values



The equation of the line into point slope form is equal to
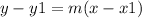
we have

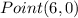
substitute
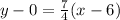

Multiply by
 both sides
both sides
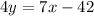
convert in standard form
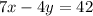
Part 2) Determine the standard form of the equation of the line that passes through
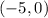 and
and

we know that
The formula to calculate the slope between two points is equal to

Substitute the values


The equation of the line into point slope form is equal to
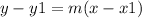
we have


substitute

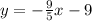
Multiply by
 both sides
both sides
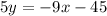
convert in standard form
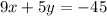
Part 3) Determine the standard form of the equation of the line that passes through
 and
and
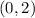
we know that
The formula to calculate the slope between two points is equal to

Substitute the values


The equation of the line into point slope form is equal to
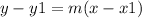
we have

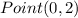
substitute


Multiply by
 both sides
both sides

convert in standard form

Part 4) Determine the standard form of the equation of the line that passes through
 and
and

we know that
The formula to calculate the slope between two points is equal to

Substitute the values


The equation of the line into point slope form is equal to
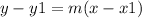
we have

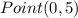
substitute


Multiply by
 both sides
both sides

convert in standard form