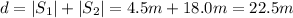Question

3.An object moves with constant acceleration 4.00 m/s2 and over a time interval reaches a final velocity of 12.0 m/s.. a.If its original velocity is 6.00 m/s, what is its displacement during the time interval?. b.What is the distance it travels during this interval?. c.If its original velocity is -6.00 m/s, what is its displacement during this interval?. d.What is the total distance it travels during the interval in part (c)?.

Answer 1

a) First of all, you need to find out the time. When a is constant, it can be calculated with this formula: a=(vf-vo)/t So you can find t like this: t=(vf-vo)/a=(12.00m/s-6.00m/s)/(4.00m/s^2)=1.50s There are several different methods to find the displacement knowing t. One of them uses the uniformly accelerated linear movement formula: d=1/2*a*t^2+vo*t=1/2*4.00m/s^2*(1.50s)^2+(6.00m/s)*1.50s=13.5m b) In this case, displacement and distance are the same thing. So the distance is also 13.5m. c) and d) This time displacement and distance are not the same thing. Take a look at the signs: Velocity starts being negative and later it becomes positive. This means the object is first going backwards while it is slowing down, and when it reaches v=0, it accelerates to the other side. Let’s find out how much time it needs to reach v=0 t=(vf-vo)/a=(0m/s-(-6.00m/s))/(4.00m/s^2)=1.50s d=1/2*4.00m/s^2*(1.50s)^2+(-6m/s)*1.50s=-4.5m So the distance during this period is -4.50m, but the displacement is always considered positive, so it is 4.50m. Let’s find out how much time it needs to reach v=12.0m/s t=(vf-vo)/a=(12.0m/s-(0m/s))/(4.00m/s^2)=3.00s Now the distance will be: d=1/2*4.00m/s^2*(3s)^2+(0m/s)*3.00s=18.0m And this time it is positive, so the displacement is also 18.0m. So the total displacement is: 4.50m+18m=22.5m And the total distance is: -4.50m+18m=13.5m There is another different method to calculate the distance, which doesn’t work for calculating the displacement (take a look at the signs and compare them). It consists on using just the initial velocity and the final velocity with the uniformly accelerated linear movement formula, without using 0 as an “intermediary”. t=(vf-vo)/a=(12.0m/s-(-6.00m/s))/(4.00m/s^2)=4.5s d=1/2*4.00m/s^2*(4.5s)^2+(-6m/s)*3.00s=22.5m You can see the result is equal to the distance we have calculated with the previous method, but it is not the same number we calculated for the displacement. Also keep in mind that each term of this last method is also different to each displacement we calculated before (before adding them).

Answer 2

(a) The motion of the object is a uniformly accelerated motion, with constant acceleration. Both the initial and final velocities are positive: this means that the object moves always in the same direction, so the displacement and the distance in this case are equal.

We can find the displacement using the equation:

`v^2 -u^2 =2aS` (1)

where

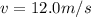`v=12.0 m/s` is the final velocity

`u=6.0 m/s` is the initial velocity

`a=4.0 m/s^2` is the acceleration

S is the displacement

By rearranging the formula and substituting the numbers, we find the displacement:

`S=(v^2-u^2)/(2a)=((12.0 m/s)^2-(6.0 m/s)^2)/(2(4.0 m/s^2))=13.5 m`

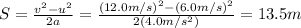
(b) As we said in the previous point, the displacement and the distance in this part of the problem are equal, so the distance travelled by the object is

`d=S=13.5 m`

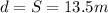
(c) In this case, the initial velocity is

`u=-6.0 m/s`

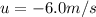
while the final velocity is

`v=12.0 m/s`

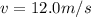
the two quantities have opposite sign: this means that at the beginning, the object is travelling in the negative direction, while later it travels in the positive direction. To find the displacement, we must calculate the distance travelled in the negative direction (until the object reaches velocity v=0) and then the distance travelled in the positive direction (from u=0 to v=12 m/s), and then calculate the difference between them.

We can still use the equation (1). The distance travelled in the negative direction can be found by using
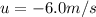`u=-6.0 m/s` and
`v=0`:

`S_1=(v^2-u^2)/(2a)=(0-(-6.0 m/s)^2)/(2(4.0 m/s^2))=-4.5 m`

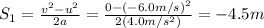
The distance travelled in the positive direction can be found by using
`u=0` and
`v=12.0 m/s`:

`S_2 =(v^2-u^2)/(2a)=((12.0 m/s)^2-0)/(2(4.0 m/s^2))=18.0 m`

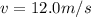Therefore, the displacement of the object is

`S=S_1 +S_2 = -4.5 m+18.0 m=13.5 m`

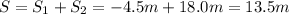
(d) The total distance is instead the sum of the distances travelled in the negative direction and in the positive direction, so:

`d=|S_1|+|S_2|=4.5 m+18.0 m=22.5 m`