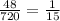Question

Six​ people, call them​ A, B,​ C, D,​ E, and​ F, are randomly divided into three groups of two. Find the probability that A and B are in the same​ group, as are C and D.​ (Do not impose unwanted ordering among​ groups.)

Answer 1

First lets find the number of permutations of three ordered groups, A and B, C and D and E and F:
3P3 = 6
However when the order in each of the pairs can be reversed, the number of arrangements meeting the required grouping becomes:
6 * 8 = 48.
The total number of permutations of the 6 people is given by:
6P6 = 720.
Therefore the required probability is found from:

`(48)/(720) = (1)/(15)`