Question

Write an exponential function to describe the given sequence of numbers. 9, 18, 36, 72, 144, ... The exponential function is y= (Use integers or fractions for any numbers in the expression.)

Answer 1

The general formula for this exponential sequence is

`y=9(2)^(x-1)`

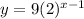
x = 1, 2, 3, 4....

Step-by-step explanation

We can see that this sequence has each of the next term being 2 multiplied by the previous term.

9, 18, 36, 72, 144....

So, we will treat the exponential sequence as a geometric sequence.

The general formula for the nth term of a geometric sequence is

aₙ = arⁿ⁻¹

`a_n=ar^(n-1)`

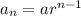
where

aₙ = nth term

a = first term = 9

r = common ratio = (Second term)/(First term) = (Third term)/(Second term) etc

r = (18/9) = (36/18) = (72/36) = (144/72) = 2

n = number of terms

So, the general formula for this exponential sequence will be

aₙ = arⁿ⁻¹

a = 9

r = 2

aₙ = 9 (2)ⁿ⁻¹

`a_n=ar^(n-1)`

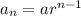
So, if we replace the nth term with the xth term, we can say

y = 9 (2)ˣ⁻¹

Hope this Helps!!!