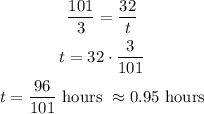Question

Adrian can complete 14 problems in 1.2 hours, and Abbi can complete 11 problems in 0.5 hours. How long would it take them to complete 32 problems, if they work together?

Answer 1

T=96/101 hours (in fraction)
In decimals its 0.95 hours

Answer 2

The rate of completed problems can be calculated using the equation:

`r=\frac{\#\text{ of problems}}{t}`

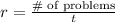
Then, for Adrian and Abbi:

`\begin{gathered} r_{\text{Adrian}}=(14)/(1.2h)=(35)/(3)\text{ problems per hour} \\ r_{\text{Abbi}}=(11)/(0.5h)=22\text{ problems per hour} \end{gathered}`

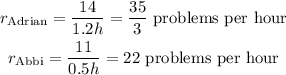
If they work together, the total rate will be the sum of the individual rates:

`r_{\text{Total}}=(35)/(3)+22=(101)/(3)\text{ problems per hour}`

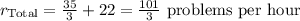
We know the rate and the number of problems (32), so using the equation for the rate:

`\begin{gathered} (101)/(3)=(32)/(t) \\ t=32\cdot(3)/(101) \\ t=(96)/(101)\text{ hours }\approx0.95\text{ hours} \end{gathered}`