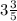Question

Joe mowed 1 1/2 lawns in 2 1/2 hours. How many complete lawns can Joe mow in 6 hours?

Answer 1

Given:

`1(1)/(2)lawns\text{ in 2}(1)/(2)hours`

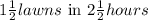
Let's find how many complete lawns Joe can mow in 6 hours.

We have:

`\begin{gathered} 1(1)/(2)lawns=2(1)/(2)\text{ hours} \\ \\ x\text{ lawns = 6 hours} \end{gathered}`

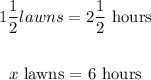
Rewrite the fractions as decimals:

`\begin{gathered} 1.5\text{ lawns = }2.5\text{ hours} \\ \\ x\text{ lawns = 6 hours} \end{gathered}`

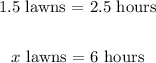
Let's solve for x.

Now, we have the proportionality equation:

`(1.5)/(2.5)=(x)/(6)`

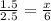
Cross multiply:

`\begin{gathered} 2.5x=6(1.5) \\ \\ 2.5x=9 \end{gathered}`

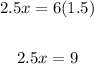
Divide both sides by 2.5:

`\begin{gathered} (2.5x)/(2.5)=(9)/(2.5) \\ \\ x=3.6=3(6)/(10)=3(3)/(5)lawns \end{gathered}`

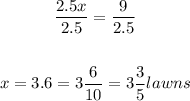
Therefore, Joe can complete 3 3/5 lawns in 6 hours.

ANSWER:

`3(3)/(5)`