Answer:
The polynomial which is factored completely is
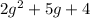 as these are not further factored.
as these are not further factored.
Explanation:
To find : Which polynomial is factored completely?
Solution :
We factor the given polynomial one by one,
1)
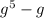
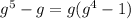
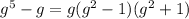
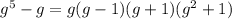
2)
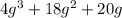
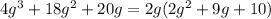
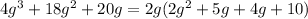
![4g^3 + 18g^2+20g=2g[g(2g+5)+2(2g+5)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/gvrw5kauzezo0izgwz5n74sd52vb1mtkeo.png)
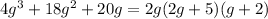
3)
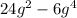

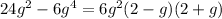
4)
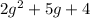
This expression is can not be factored with rational number as
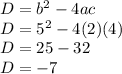
Discriminant D<0 so there is no rational roots.
So, The polynomial which is factored completely is
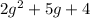 as these are not further factored.
as these are not further factored.