Question

Which polynomial is prime?

7x2 – 35x + 2x – 10
9x3 + 11x2 + 3x – 33
10x3 – 15x2 + 8x – 12
12x4 + 42x2 + 4x2 + 14

Answer 1

1.

`7x^2-35x + 2x - 10=7x^2-33x-10,\\ D=(-33)^-4\cdot 7\cdot (-10)=1369,\\ √(D)=37,\\ \\ x_1=(33-37)/(2\cdot 7)=-(2)/(7),\ x_2=(33+37)/(2\cdot 7)=5,\\ \\ 7x^2-35x + 2x - 10=7x^2-33x-10=7(x+(2)/(7))(x-5)=(7x+2)(x-5)` - this polynomial is not prime.

3.

`10x^3 - 15x^2 + 8x- 12=(10x^3-15x^2)+(8x-12)=5x^2(2x-3)+4(2x-3)=(2x-3)(5x^2+4)` - this polynomial is not prime.

4.

`12x^4 + 42x^2 + 4x^2 + 14=12x^4+46x^2+14=2(6x^4+23x^2+7),\\D=23^2-4\cdot 6\cdot 7=361, √(D)=19,\\ \\x_1^2=(-23-19)/(12) =-(7)/(2) , x_2^2=(-23+19)/(12)=-(1)/(3) ,\\ \\ 12x^4 + 42x^2 + 4x^2 + 14=2(6x^4+23x^2+7)=12(x^2+(7)/(2))(x^2+(1)/(3))` - this polynomial is not prime.

2. This polynomial is prime.

Answer 2

Option 2 is correct.

Step-by-step explanation:

Given the polynomials we have to choose the polynomial which is prime.

A polynomial with integer coefficients that cannot be factored into lower degree polynomials are Prime polynomials.

`7x^2 - 35x + 2x - 10`

⇒
`7x(x-5)+2(x-5)`

⇒
`(7x+2)(x-5)`

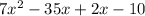
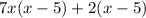
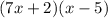
can be factored ∴ not a prime polynomial.

`9x^3 + 11x^2 + 3x - 33`

⇒
`x^2(9x+11)+3(x-11)`

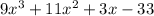
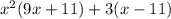
cannot be factored ∴ prime polynomial.

`10x^3 - 15x^2 + 8x - 12`

⇒
`5x^2(2x-3)+4(2x-3)`

⇒
`(5x^2+4)(2x-3)`

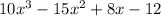
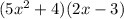
can be factored ∴ not a prime polynomial.

`12x^4 + 42x^2 + 4x^2 + 14`

⇒
`6x^2(2x^2+7)+2(2x^2+7)`

⇒
`(6x^2+2)(2x^2+7)`

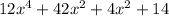
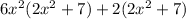
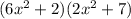
can be factored ∴ not a prime polynomial.

The second polynomial can not be factored into lower degree polynomial therefore, prime polynomial.