we know that
The zeros of the function are the values of x when the value of the function is equal to zero
so
Let's verify each case to determine the solution.
Substitute the value of
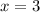 and
and
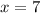 in each function and then verify the value of the function
in each function and then verify the value of the function
case A)

For
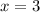

therefore
the value of
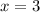 is a zero of the function
is a zero of the function
For
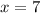

therefore
the value of
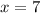 is not a zero of the function
is not a zero of the function
The case A) is not the solution
case B)

For
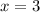

therefore
the value of
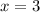 is not a zero of the function
is not a zero of the function
For
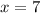

therefore
the value of
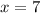 is a zero of the function
is a zero of the function
The case B) is not the solution
case C)

For
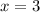

therefore
the value of
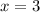 is a zero of the function
is a zero of the function
For
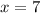

therefore
the value of
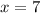 is a zero of the function
is a zero of the function
The case C) is a solution
case D)

For
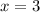

therefore
the value of
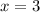 is not a zero of the function
is not a zero of the function
For
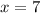

therefore
the value of
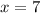 is not a zero of the function
is not a zero of the function
The case D) is not a solution
therefore
The answer is
