Question

Find the 6th term in the geometric sequence with t3 = 150 and t5 = 3750.

Answer 1

The 6th term in the geometric sequence is either 18750 or -18750.

Explanation:

Given information: In the given GP

`t_3=150`

`t_5=3750`

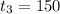
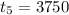
The nth term of a GP is

`t_n=ar^(n-1)`

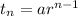
where, a is first term and r is common ratio.

Third term of the GP is 150, so

`t_3=ar^(3-1)`

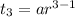
`150=ar^2` .... (1)

Fifth term of the GP is 3750, so

`t_5=ar^(5-1)`

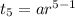
`3750=ar^4` .... (2)

Divide equation (2) by equation (1).

`(3750)/(150)=(ar^4)/(ar^2)`

`25=r^2`

`\pm 5=r`

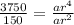
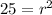
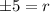
The value of common ratio is either 5 or -5.

Put the value of r² in equation (1).

`150=a(25)`

`6=a`

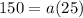
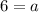
The first term of the GP is 6.

If the first term of GP is 6 and common difference is 5, then 6th term is

`t_6=ar^(6-1)=ar^5=6(5)^5=18750`

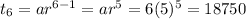
If the first term of GP is 6 and common difference is -5, then 6th term is

`t_6=ar^(6-1)=ar^5=6(-5)^5=-18750`

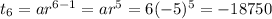
Therefore the 6th term in the geometric sequence is either 18750 or -18750.

Answer 2

Determine first the common ratio (r) of the geometric sequence by,

r = (t5 / t3)^(1/(5 - 3))

Substituting the known values from the given,

r = (3750 / 150)^(1/2) = 5

The sixth term may be obtained by multiplying the fifth term (t5 = 3750) by the common ratio. This is shown below,

t6 = (3750) x 5 = 18750

Thus, the 6th term of the geometric sequence is 18750.