Question

It takes a boat 2 hours to travel 24 miles downstream and 4 hours to travel 24 miles upstream.What is the speed of the boat in still water?What is the speed of the current of the river?

Answer 1

Let the speed of Boat is B and speed of stream is S

The expression for Speed is :

`\text{ Spe}ed=(Dis\tan ce)/(Time)`

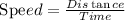
Time taken by the boat to travel 24 miles downstream is 2 hours

So, speed of boat in downtsream :

`\begin{gathered} \text{ Spe}ed\text{ of Boat during Downstream = }(24)/(2) \\ \text{Spe}ed\text{ of Boat during Downstream = 12 miles/hr} \end{gathered}`

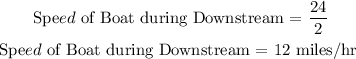
Time taken by the boat tp travel 24 miles upstream is 4 hours

`\begin{gathered} \text{Spe}ed\text{ of Boat during Upstream = }(24)/(4) \\ \text{Spe}ed\text{ of Boat during Upstream = 6 miles/hr} \end{gathered}`

Downstream means : A boat is said to go downstream if it is moving along the direction of the stream i.e net speed is the sum of speed of boat + Speed of river

From the data :

Speed of Boat + Speed of stream = 12

B + S = 12 (1)

Upstream Means : If the boat is flowing in the opposite direction to the stream, it is called upstream.i.e. the net speed is the difference of speed of baot and river

From the given data : Speed of Boat - Speed of stream = 6

B - S = 6 (2)

Simplify the equation (1) & (2)

B + S = 12

B - S = 6

Add the equations :

B + S + B - S = 12 + 6

2B = 18

B = 18/2

B = 9

i.e. Speed of Boat is 9 miles/hr

Substitute B = 9 in the equation (1)

B + S = 12

9 + S = 12

S = 12 - 9

S = 3 miles/hr

Speed of stream of current water is 3 miles/hr

Answer : Speed of boat in still water is 9 miles/hr

speed of the current of the river is 3 miles/hr