Question

The center of a circle is at the origin. An endpoint of a diameter of the circle is at (-3, -4). How long is the diameter of the circle?

Answer 1

Use the distance formula

`√((-4-4)^2+(-3-3)^2) = √(100)=10`

Answer 2

The length of the diameter of the circle is 10 unit.

Explanation:

Given : The center of a circle is at the origin. An endpoint of a diameter of the circle is at (-3, -4).

To find : How long is the diameter of the circle?

Solution :

The center of a circle is at the origin i.e.
`C=(x_1,y_1)=(0,0)`

An endpoint of a diameter of the circle is at
`D=(x_2,y_2)=(-3,-4)`

The distance between the center and the end point of the diameter is the radius of the circle.

So, we find the radius with the help of distance formula,

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

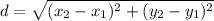
Substitute the value in the formula,

`r=√((-3-0)^2+(-4-0)^2)`

`r=√(9+16)`

`r=√(25)`

`r=5`

Diameter is twice of radius
`d=5* 2=10`

Therefore, The length of the diameter of the circle is 10 unit.