Answer:
a. Shift left.
b. Shift left.
c. Shift left.
d. Shift right.
e. No change,
Step-by-step explanation:
Let's remember Le Chatelier's Principle: Le Chatelier's principle states that if a dynamic equilibrium is disturbed by changing conditions, the position of equilibrium shifts to counteract the change to re-establish an equilibrium.
Let's write the reaction:
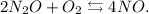
Now, let's analyze each statement:
a. We can apply pressure because all species in the reaction are in the gas phase. Remember that increasing the pressure on a gas reaction shifts the position of equilibrium towards the side with fewer moles of gas molecules. You can see in the reaction that on the left side we have 3 moles in total, but on the right side, we have 4 moles in total, so the equilibrium goes to the left. Shift left.
b. If we reduce the concentration of a substance in a reaction, in this case, O2 as the reactant, we will not increase the concentration of the products, so the equilibrium goes to the left. Shift left.
c. If we add NO, we will increase the concentration of N2O and O2, so in this case, the equilibrium goes to the left. Shift left.
d. This situation is similar to the last, but, we are on the other side. Increasing the concentration of N2O will increase the concentration of NO, so the equilibrium goes to the right. Shift right.
e. Remember that adding a catalyst makes absolutely no difference to the position of equilibrium, and Le Châtelier's principle does not apply. Based on this logic, there's no change.