Question

You are asked to build an open cylindrical can with volume 180.5 cubic inches. You will cut the bottom from a square of metal and form the curved side by bending a rectangular sheet of metal. . . Find the exact value of the radius and height of the can that will minimize the total amount of material required for the square and the rectangle.

Answer 1

In order to derive the function o f the height of the cylinder, you will use this formula

V=πr2h

h=d h=d=2r h=2r

V=πr22r

V(r,h)=180.5=πr2h⟹h=180.5πr2

⟹A(r)=r(r+h)=r2+180.5πr

Then you can derive the function, however there would be changes in the height and radius,considering that the volume is constant. There is also another way of solving it

The function should be

A(r)=2r(2r+h)=4r2+361πr

A′(r)=8r−361πr2

Answer 2

The volume of cylinder is

`V=\pi r^2h=180.5.`

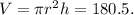
Express h from this expresiion:

`h=(180.5)/(\pi r^2).`

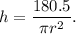
The full surface area of this cylinder is

`A=2\pi r^2+2\pi rh.`

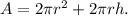
Then in terms of r the area is

`A(r)=2\pi r^2+2\pi r\cdot (180.5)/(\pi r^2)=2\pi r^2+(361)/(r).`

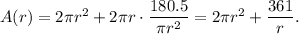
Find the derivative
`(dA)/(dr):`

`(dA)/(dr) =4\pi r-(361)/(r^2).`

Equate
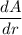`(dA)/(dr)` to zero:

`4\pi r-(361)/(r^2)=0,\\ \\4\pi r^3=361,\\ \\ r=\sqrt[3]{(361)/(4\pi)} \approx 28.74.`

When
`r<\sqrt[3]{(361)/(4\pi)}`, the derivative
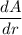`(dA)/(dr)` is <0 (area is decreasing) and when
`r>\sqrt[3]{(361)/(4\pi)}`, the derivative
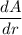`(dA)/(dr)` is >0 (area is increasing). This means that
`r=\sqrt[3]{(361)/(4\pi)}` is point of minimum.

Thus,

`h=(180.5)/(\pi r^2)=\frac{180.5}{\pi (\sqrt[3]{(361)/(4\pi)})^2}\approx 6.13.`

Answer: the approximate values: r≈28.74 in, h≈6.13 in. and the exact values:

`r=\sqrt[3]{(361)/(4\pi)}` in,

`h=\frac{180.5}{\pi (\sqrt[3]{(361)/(4\pi)})^2}` in.