Question

Describe how the transformed function below is obtained from its parent function. . y=(x-10)^3. . a.The parent function y=x^3 is shifted 10 units to the right. b.The parent function y=x^3 is shifted 10 units to the left.. c.The parent function y=(-x)^3 is strectched vertically by a factor of 10.. d.The parent function y=x^3 is shifted 10 units down.

Answer 1

Option a is correct

The parent function y=x^3 is shifted 10 units to the right.

Explanation:

Horizontal shift:

If a parent function y = f(x);

then; the transformation y = f(x+h) is either horizontal right or left.

If h < 0, then the shift is h units right

If h > 0, then the shift is h units left

As per the statement:

The transformed function below is obtained from its parent function
`y=x^3` is:

`y = (x-10)^3`

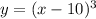
By definition of horizontal shift:

h = -10 < 0

⇒so the graph is shifted to 10 units right

Therefore, The parent function y=x^3 is shifted 10 units to the right.

Answer 2

The correct answer to this question is: "a.The parent function y=x^3 is shifted 10 units to the right."

Nothing is being added to y to move it up or down.

Nothing is multiplying y to stretch it.

The only thing that is modified is the x values .. which determine right and left positions