Answer:
Variables: C = price of a cookie in dollars, B = price of a brownie in dollars
Equation for day 1 : 14c + 6b = 32
Equation for day 2: c + 2b = 86
Cookies cost $0.76 each and brownies cost $3.55 each
Step-by-step explanation:
Here, we want to get the cost of each of the treats
Let the price of cookies be $b and the price of brownies be $b
On the first day, they sold 14 cookies, which is a total of $14 * c = $14c , and 6 brownies which is $b * 6 = $6b
The sum of these two is $32. Mathematically, we have this as:
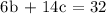
On the second day, 1 cookie ($c) and 24 brownies (24 * $b = $24b). The sum of these two is $86
We can write the equation as:
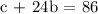
We have the two equations as follows:
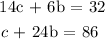
By using elimination, we multiply the first equation by 4 and the second by 1
We have this as:
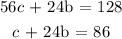
We subtract equation ii from i:

Finally, we get the value for a brownie by making a substitution into any of the two initial equations:
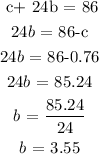
Now, let us fill in the answers as required by the question:
Variables: C = price of a cookie in dollars, B = price of a brownie in dollars
Equation for day 1 : 14c + 6b = 32
Equation for day 2: c + 2b = 86
Cookies cost $0.76 each and brownies cost $3.55 each