Question

3, A baseball batter comes to bat 5 times. The probability of ahit is 1/5(=0.20). What is the probability of getting at least 4 hits? (Find the exact number.)

Answer 1

We define event A as:

A: The baseball batter hit the ball

The probability of a hit (a success) is p = 0.20. The batter comes to a bat 5 times, so we have the binomial distribution:

`P(X=x)=C^n_x\cdot p^x\cdot(1-p)^(n-x)`

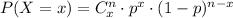
Where C is the combination operator, x is the number of successes out of n trials (5 in this case), and p is the probability of success. Then, to find the probability of getting at least 4 hits, this means that we need to find the probabilities of x = 4 and x = 5 and then add them.

For x = 4:

`P(X=4)=C^5_4\cdot0.20^4\cdot(1-0.20)^(5-4)=5\cdot0.20^4\cdot0.8^1=0.0064`

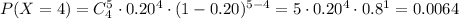
Now, for x = 5:

`P(X=5)=C^5_5\cdot0.20^5\cdot(1-0.20)^(5-5)=1\cdot0.20^5\cdot0.8^0=0.00032`

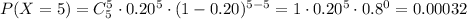
Finally, the probability of getting at least 4 hits is:

`P(X\ge4)=P(X=4)+P(X=5)=0.0064+0.00032=0.00672`