Question

A ramp leads up to a building. The top of the ramp is 4 feet above the ground, and the bottom of the ramp is 18 feet from the building, as shown.

what is the length of the ramp? Round your answer to the nearest tenth of a foot.

A. 22 ft
B. 18.4 ft
C. 20 ft
D. 19.4 ft

Answer 1

Pythagoras,
(inclined length)^2 = height^2+length^2
=4'^2+18'^2
=16+324
=338
Inclined length = sqrt(338)=18.38'

Answer 2

The correct option is B.

Explanation:

It is given that top of the ramp is 4 feet above the ground and the bottom of the ramp is 18 feet from the building.

Draw a figure by using the given information.

From the figure it is clear than it is a right angled triangle with base 18 feet and height 4 feet.

According to the Pythagoras theorem,

`hypotenuse^2=perpendicular^2+base^2`

Using the Pythagoras theorem, the length of ramp is

`AC^2=AB^2+BC^2`

`AC^2=4^2+(18)^2`

`AC^2=16+324`

`AC^2=340`

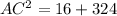
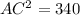
Taking square root both the sides.

`AC=√(340)`

`AC=18.439`

`AC\approx 18.4`

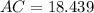
The length of the ramp is 18.4 ft. Therefore the correct option is B.