Question

A basketball player makes 70% of the free throws he shoots. Suppose that he tries 15 free throws.

Answer 1

a. 95%

b. 10.5

c. 1.77

Step-by-step explanation:

To find the probability that x shots are successful from n trials, we will use the following equation for the binomial distribution

`\begin{gathered} P(x)=nCx\cdot p^x\cdot(1-p)^(n-x) \\ \text{ Where nCx = }(n!)/(x!(n-x)!) \end{gathered}`

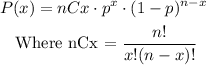
In this case, n = 15 free throws, p = 70% which is the probability of success, and we need to calculate the probability that he will make more than 7 throws, so x > 7. Then, the probability is equal to

`\begin{gathered} P(x>7)=P(8)+P(9)+P(10)+P(11)+...+P(15) \\ P(x>7)=\sum_{x\mathop{=}8}^(15)15Cx\cdot0.7^x\cdot(1-0.7)^(15-x) \\ \\ P(x>7)=0.95=95\text{ \%} \end{gathered}`

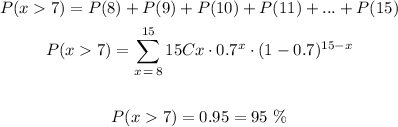
Additionally, the expected value and the standard deviation for a binomial probability are equal to

`\begin{gathered} E(x)=np \\ S(x)=√(np(1-p)) \end{gathered}`

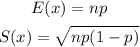
So, replacing n = 15, and p = 0.7, we get:

`\begin{gathered} E(x)=15(0.7)=10.5 \\ S(x)=√(15(0.7)(1-0.7))=1.77 \end{gathered}`

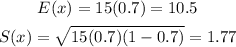
Therefore, the answers are

a. 95%

b. 10.5

c. 1.77