Question

Annie needs $30 to buy a coat. She has saved $12 and plans to work as a babysitter to earn $6 per hour. Which inequality shows the minimum number of hours, n, that Annie should work as a babysitter to earn enough to buy the coat?

12 + 6n ≤ 30, so n ≤ 3

12 + 6n ≥ 30, so n ≥ 3

6n ≥ 30 + 12, so n ≥ 7

6n ≤ 30 + 12, so n ≤ 7

Answer 1

(B)12 + 6n ≥ 30, so n ≥ 3

Explanation:

Annie already has $12

Let n be the number of hours she needs to work

If she earns $6 per hour

Her Income in n hours = $6 X n =$6n

Total Amount Annie has = 12 + 6n

Since she needs $30 to buy a coat, her total income must not be less than $30.

Therefore:

`12 + 6n\geq 30`

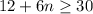
is the inequality which shows minimum number of hours, n, that Annie should work as a babysitter to earn enough.

Next, we solve
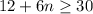`12 + 6n\geq 30` for n.

`12 + 6n\geq 30`

`6n\geq 30-12\\ 6n\geq 18\\`

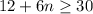
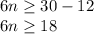
Divide both sides by 6

`n\geq 3`

Answer 2

Annie's total earnings from her initial savings, $12, and from babysitting should be equal or more than 30. Annie's total earnings from babysitting may be expressed as $6n. The inequality should be,

12 + 6n ≥ 30

Solving for x,
6n ≥ 30 - 12

6n ≥ 18 ; n ≥ 3

Thus, the answer is the second among the choices.