Answer:
Option (b) is correct.
35th term of an arithmetic sequence is 197.
Explanation:
Given :

We have to find the 35 term of an arithmetic sequence whose

For an Arithmetic sequence the general term is given as
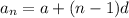 ,
,
where a is first term ,
n is number of term
d is common difference,
Thus, the 18th term
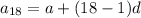
We have
 , solving for d , we have,
, solving for d , we have,

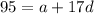
Thus,
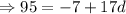
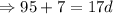
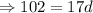
Divide both side by 17, we get,
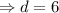
Now, 35th term of an arithmetic sequence is given by,
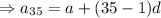
Substitute, a and d , we get,
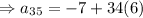
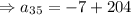
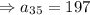
Thus, 35th term of an arithmetic sequence is 197.
Option (b) is correct.