Question

What is the 32nd term of the arithmetic sequence where a1 = 12 and a13 = -60

Answer 1

- 174

Explanation:

The nth term of an arithmetic sequence is given as

Tn = a + (n - 1)d

where Tn is the nth term

a is the first term , n is the number of term and d is the common difference. As such,

a13 = a + (13 - 1)d

= a + 12d

Given that a1 = 12 and a13 = -60

-60 = 12 + 12d

12d = -72

d = -6

Hence a32 which is the 32nd term

= 12 + (32 - 1)-6

= 12 + (-186)

= - 174

Answer 2

The 32nd term of Arithmetic sequence is -174

Explanation:

Given:
`a_1=12, a_(13)=-60`

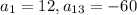
We are given two term of the Arithmetic sequence.

Formula:

`a_n=a+(n-1)d`

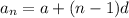
For
`a_1=12`

`a=12`

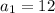
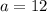
For
`a_(13)=-60`

`a+12d=-60`

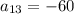
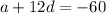
Using two equation solve for a and d

`12+12d=-60`

`1+d=-5`

`d=-6`

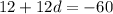
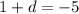
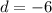
We need to find 32nd term

`a_(32)=a+31d`

`a_(32)=12+31(-6)`

`a_(32)=12-186`

`a_(32)=-174`

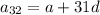
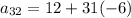
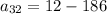
Hence, The 32nd term of Arithmetic sequence is -174