Question

Which statement is correct with respect to f(x) = -3|x − 1| + 12?

The V-shaped graph opens upward, and its vertex lies at (-3, 1).



The V-shaped graph opens downward, and its vertex lies at (-1, 3).



The V-shaped graph opens upward, and its vertex lies at (1, -12).



The V-shaped graph opens downward, and its vertex lies at (1, 12).

Answer 1

Hello,

Answer D
y is max if |x-1|=0==>x=1 and y=0+12=12

Answer 2

Answer: The correct option is

(D) The V-shaped graph opens downward, and its vertex lies at (1, 12).

Step-by-step explanation: We are given to select the correct statement about the graph of the following function :

`f(x)=-3|x-1|+12~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We know that

a function with a V-shaped graph having vertex at (h, k) is of the form :

`f(x)=a|x-h|+k,`

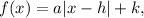
if a < 1, then it opens downwards and id a > 1, then it opens upwards.

Comparing the given equation (i) with the standard form, we get

the graph will be a V-shaped with vertex at the point (1,12) and since a = -3 < 1, so the graph will open downwards.

Thus, the V-shaped graph opens downward, and its vertex lies at (1, 12).

Option (D) is CORRECT.