Question

Given a soda can with a volume of 36 and a diameter of 4, what is the volume of a cone that fits perfectly inside the soda can? (Hint: only enter numerals in the answer blank).

Answer 1

For this case what we should do is model the soda can as a cylinder.

We have then:

`image`

Where,

r: can radius

h: height of the can

From here, we clear the value of the height:

`image`

Substituting values we have:

`image`

We are now looking for the volume of the cone.

We have then:

`image`

Substituting values we have:

`image`

Answer:

the volume of a cone that fits perfectly inside the soda can is:

`V = 12.02`

Answer 2

First we need to find the heigh of the soda can be rearanging the volume formula,
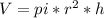
`V = pi * r^2* h`. We can make that
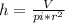
`h = (V)/(pi * r^2)` We know that V is 36 and radius is half of the diameter, so radius is 2.
`h = (36)/(pi * 2^2)`

`h = (36)/(pi * 4)`
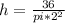
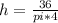
h = 2.87

Now, we can use the height to figure out the volume of a cone. The volume of a cone is
`V = pi * r^2 * (h)/(3)`
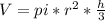
R is 2 again and h is 2.87

`V = pi * 2^2 * (2.87)/(3)`

`pi * 4 * .96`
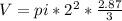
12.56*.96 = 12.0576
So a cone with a volume of 12.0576 is the largest that will fit into the soda can