Question

How many solutions does this linear system have?

y = 2x – 5

–8x – 4y = –20

Answer 1

Hello,

One solution (5/2,0)

since
y=2x-5==>2x-y=5 (1)
-8x-4y=-20==>2x+y=5(2)
(1)+(2)==>4x=10==>x=5/2
y=2*5/2-5==>y=0

Answer 2

Given linear system of equation has only 1 solution.

Explanation:

Given System of linear equation is,

y = 2x - 5

-8x - 4y = -20

rewriting the given system in standard form,

2x - y - 5 = 0

-8x - 4y + 20 = 0

We know that number of solution of the system of equation is determined by comparing the ratios of coefficient and constant term.

here coefficient of x that is
`a_1=2\:,\:a_2=-8`

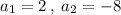
coefficient of y that is
`b_1=-1\:,\:b_2=-4`

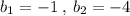
constant term that is
`c_1=-5\:,\:c_2=20`

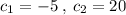
we have,

`(a_1)/(a_2)=(2)/(-8)=(-1)/(4)\:\:,\:\:(b_1)/(b_2)=(-1)/(-4)=(1)/(4)\:\:and\:\:(c_1)/(c_2)=(-5)/(20)=(-1)/(4)`

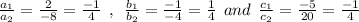
Since,
`(a_1)/(a_2)\\eq(b_1)/(b_2)`

We only have one unique solution.

Therefore, Given linear system of equation has only 1 solution.