Question

Problem 2:Two bumper cars, one blue(left) and one orange(right), at an amusement park ridecollide as shown below.7 ft118°5.5 fta. How far apart d were the two cars before they collided?b. Before the collision, a third red car was 10 feet from the blue car and 13feet from the orange car. Describe the angles formed at all three cars beforethe collision.

Answer 1

Part A. In the given problem a triangle is formed. Since we are required to determine one of its sides given the opposite angle and the other two sides we can use the cosine law:

`c^2=a^2+b^2-2ab\cos\theta`

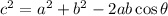
Where:

`\begin{gathered} c,a,b\text{ = sides} \\ \theta=\text{ opposite angle} \end{gathered}`

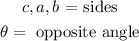
Now, we plug in the values:

`d^2=7^2+5.5^2-2(7)(5.5)\cos118`

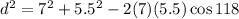
Now, we solve the operations:

`d^2=115.4`

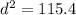
Now, we take the square root to both sides:

`\begin{gathered} d=√(115.4) \\ d=10.7 \end{gathered}`

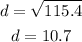
Therefore, the distance between the cars is 10.7 feet.

Part B. We are given the following situation:

We will apply the coside law using the angle "x" as the opposite angle:

`10.7^2=10^2+13^2-2(10)(13)\cos x`

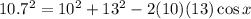
Now, we solve the operations:

`114.49=100+169-260\cos x`

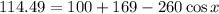
Now, we solve the addition:

`114.49=269-260\cos x`

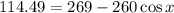
Now, we subtract 269 from both sides:

`\begin{gathered} 114.49-269=-260\cos x \\ -145.51=-260\cos x \end{gathered}`

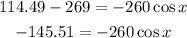
Now, we divide both sides by -260:

`(-145.51)/(-260)=\cos x`

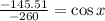
Now, we take the inverse function of the cosine:

`\cos^(-1)((-145.51)/(-260))=x`

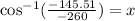
Solving the operations:

`55.97=x`

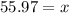
Therefore, angle "x" is 55.97 degrees.

Now, we use angle "y" as the opposite angle. Applying the cosine law we get:

`13^2=10^2+10.7^2-2(10)(10.7)\cos y`

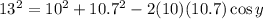
Solving the operations:

`169=214.5-214\cos y`

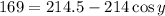
Now, we subtract 214.5 from both sides:

`\begin{gathered} 169-214.5=-214\cos y \\ -45.5=-214\cos y \end{gathered}`

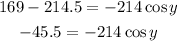
Now, we divide both sides by 214

`(-45.5)/(-214)=\cos y`

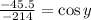
Now, we take the inverse function of the cosine:

`\begin{gathered} \cos^(-1)(-(45.5)/(-214))=y \\ \\ 77.75=y \end{gathered}`

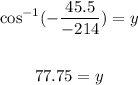
Therefore, angle "y" is 77.72 °

To determine angle "z" we will use the fact that the sum of the interior angles of a triangle always adds up to 180:

`\begin{gathered} x+y+z=180 \\ \end{gathered}`

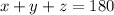
Plugging in the values:

`55.97+77.72+z=180`

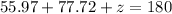
Solving the operations:

`133.69+z=180`

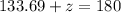
Now, we subtract 133.69 from both sides:

`\begin{gathered} z=180-133.69 \\ z=46.31 \end{gathered}`

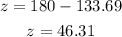
Therefore, angle "z" is 46.31 degrees.