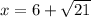Question

Solve x2 = 12x – 15 by completing the square. Which is the solution set of the equation?

Answer 1

The answer is x = 6 + √21. The general form of quadratic function is ax2 + bx + c = 0. So, the equation x2 = 12x – 15 in the general form will be look like: x2 - 12x + 15 = 0. Now, move the number term on the right side of the equation: x2 - 12x = -15. Since b = 12, (b/2)2 = (12/2)2 = (6)2 = 36. Add this number on the both side of equation: x2 - 12x + 36 = -15 + 36. From here: (x-6)2 = 21. Take square root on both sides: x - 6 = √21. Solve for x: x = 6 + √21

Answer 2

For this case we have the following polynomial:

`x ^ 2 = 12x - 15`
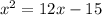
The first thing to do is to place the variables on the same side of the equation.
We have then:

`x ^ 2 - 12x = -15`
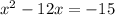
We complete the square by adding the term (b / 2) ^ 2 on both sides of the equation.
We have then:

`x ^ 2 - 12x + (-12/2) ^ 2 = -15 + (-12/2) ^ 2`
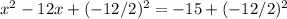
Rewriting we have:

`x ^ 2 - 12x + (-6) ^ 2 = -15 + (-6) ^ 2 x ^ 2 - 12x + 36 = -15 + 36 (x-6) ^ 2 = 21`

`x-6 =+/- √(21)`
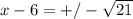
Therefore, the solutions are:

`x = 6 - √(21)`

`x = 6 + √(21)`
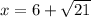Answer:
the solution set of the equation is:

`x = 6 - √(21)`

`x = 6 + √(21)`