The pattern is growing horizontally and vertically, with the shape of a ladder. Each square is a step of the ladder. Is symmetrical in its diagonal.
For figure 1, we have 1 square.
For figure 2, we have 2+1 = 3 squares.
For figure 3, we have 3+2+1 = 6 squares.
For figure 4, we have 4+3+2+1 = 10 squares.
We can also look at the pattern as joining a "tower" of squares of size "n" for figure "n".
Figure n will have:
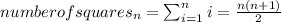
For figure 10 we have: 10*11/2 = 110/2 = 55 squares.
It will look like a triangle with 10 squares in the base and 10 squares in the left side.
For figure 55 we will have 1540 squares.

To know if 190 correspond to one figure we can calculate:
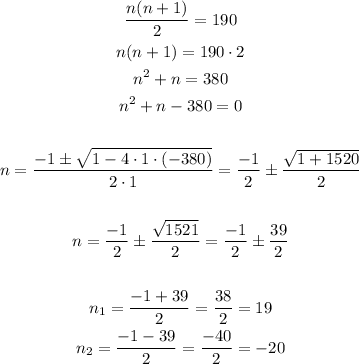
We have a solution for n=19, so in figure 19 we will have a ladder with 190 squares, as it satisfy the pattern we have figured.