Question

Lindsay is checking out books at the library, and she's primarily interested in Mysteries and nonfiction. She has narrowed her selection down to six Mysteries into 10 non-fiction books. If randomly she chooses three books from her selection, what's the probability that they will be nonfiction?As a fraction or round your answer to four decimal places, if necessary

Answer 1

She selected 6 Mystery books and 10 Non-fiction books, a total of 16 books.

You have to determine the probability that if she chooses 3 books at random, the three will be Non-fiction.

To calculate this you have to consider this scenario as choosing "without replacement" since it will make no sense for her to choose the same book 3 times.

So, the probability of choosing a Non-fiction book (N), can be expressed as:

`P(N_1\cap N_2\cap N_3)=P(N_1)\cdot P(N_2)\cdot P(N_3)`

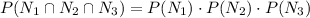
The subindices 1, 2, 3 indicate the order that the books were chosen.

-The probability of the first book being Non-fiction can be calculated as the quotient between the number of Non-fiction books and the total number of books:

`\begin{gathered} P(N_1)=\frac{nº\text{non}-\text{fiction}}{\text{total books}} \\ P(N_1)=(10)/(16) \end{gathered}`

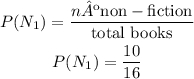
Once this book was choose, there are 15 books left to choose from, 6 of them are Mystery books and the remaining 9 are Non-fiction.

To determine the probability of the second book being Non-fiction, you have to use the information of the remaining books:

`\begin{gathered} P(N_2)=\frac{nºremaining\text{ non-fiction}}{remaining\text{ books}} \\ P(N_2)=(9)/(15) \end{gathered}`

Once this book was chosen, the remaining number of books is 14 and the remaining number of Non-fiction books is 8.

Using these values you can calculate the probability of the first book being Non-fiction

`\begin{gathered} P(N_3)=\frac{nº\text{remaining non-fiction}}{remaining\text{ }books} \\ P(N_3)=(8)/(14) \end{gathered}`

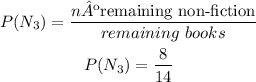
Next, you can calculate the probability that the 3 books chosen are Non-fictional:

`P(N_1\cap N_2\cap N_3)=P(N_1)\cdot P(N_2)\cdot P(N_3)=(10)/(16)\cdot(9)/(15)\cdot(8)/(14)=(3)/(14)\approx0.2143`

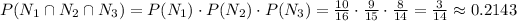
The probability of choosing 3 books at random that is Non-fiction is 3/147 or 0.2143.