Let the speed for running be x
Let the speed for cycling be y
Given that the athlete cycles 8 miles/hr faster than he runs, we have

Every morning, the athlete cycles 4 miles and runs 2.5 miles for a total of 1 hour.
This implies that the total time for cycling and running is 1 hour.
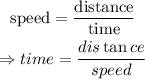
Time for cycling:
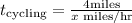
Time for running:
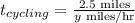
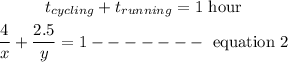
Substitute equation 1 into equation 2
![\begin{gathered} (4)/(x)+(2.5)/(y)=1 \\ (4)/(x)+(2.5)/((x+8))=1 \\ \text{LCM = x(x+8)} \\ (4(x+8)+2.5x)/(x(x+8))=1 \\ open\text{ the brackets} \\ \frac{4x+32+2.5x_{}}{x^2+8x}=1 \\ (6.5x+32)/(x^2+8x)=1 \\ \text{cross}-mul\text{tiply} \\ 6.5x+32=x^2+8x \\ \text{collect like terms} \\ x^2+8x-6.5x-32=0 \\ x^2+1.5x-32=0 \\ \end{gathered}]()
solving the quadratic equation by factorization, we have
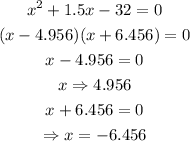
since x and y are the speeds of running and cycling, their values cannot be negative,
Thus, x= 4.956 miles/hr
Hence, they run at 4.956 miles/hr