The equation is
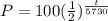
To find the original amount of carbon-14 we need to substitute t=0 in our last equation
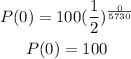
Then, the original amount of carbon-14 was 100.
To plot the solution, we need to replace the values given in the table
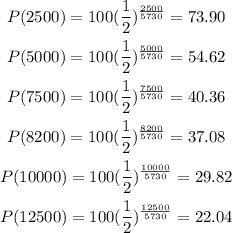
you need to replace this numbers in the table. Then, the graph is