Question

Hello, I was wondering if you could help me see if f(x) = 2/5 x + 1/3 and g(x) = 5/2 x - 5/6 are inverses of each other.

Answer 1

Given,

The expression of the function f(x) is 2/5 x + 1/3.

The expression of the function g(x) is 5/2 x - 5/6.

Required

To identify whether the function are inverse of each other.

The function is inverse of each other when f(g(x)) = x and g(f(x)) = x.

So,

`\begin{gathered} f(g(x))=f((5)/(2)x-(5)/(6)) \\ =(2)/(5)((5)/(2)x-(5)/(6))+(1)/(3) \\ =(2)/(5)*(5)/(2)x-(2)/(5)*(5)/(6)+(1)/(3) \\ =x-(1)/(3)+(1)/(3) \\ =x \end{gathered}`

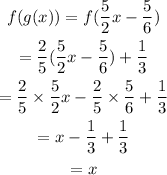
Checking for g(f(X)).

`\begin{gathered} g(f(x))=g((2)/(5)x+(1)/(3)) \\ =(5)/(2)((2)/(5)x+(1)/(3))-(5)/(6) \\ =(5)/(2)*(2)/(5)x+(5)/(2)*(1)/(3)-(5)/(6) \\ =x+(5)/(6)-(5)/(6) \\ =x \end{gathered}`

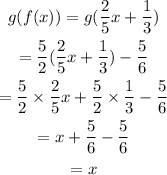
Hence, both the function are inverse of each other.