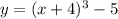Question

Which equation defines the graph of y=x^3 after it is shifted vertically 5 units down and horizontally left 4 units

A) y=(x-4)^3 - 5
B) y=(x+5)^3 - 4
C) y=(x+5)^3 + 4
D) y=(x+4)^3 - 5

Answer 1

Option D

The function shifted vertically 5 units down and horizontally left 4 units is,
`y=(x+4)^3-5`

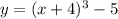
Step-by-step explanation

The function is given by, y=
`f(x)=x^3`

To move a function shift vertically 5 units down

We know that moving the function down, you subtract outside the function i.e,
`f(x)-c`;
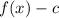`f(x)` moved down c units.

Therefore, the function f(x) vertically shift 5 units down by
`f(x)=x^3-5`

Now, to move a function horizontally 4 units left.

To shift the function left add inside the function's argument i.e,
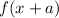`f(x+a)` gives f(x) shifted a units to the left.

so, the function f(x) horizontally left 4 units i.e, f(x+4)=
`(x+4)^3`

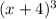
Now, the graph of the function
`y=x^3` after it is shifted vertically 5 units down and horizontally left 4 units is,
`y=(x+4)^3-5`

Answer 2

y=f(x) +k is a vertical shift down for k= - 5
y=f(x+h) is a horizontal shift left for h=4
Answer: D) y = ( x + 4 )³ - 5.