Question

Assuming 100% dissociation, calculate the freezing point and boiling point of 2.59 m K3PO4(aq).

Answer 1

The freezing point can be obtained from the formula Tf= Tf (solvent)- Kf* m* n. Kf of water is 1.85 C/m. n is equal to 4 since there are 4 ions dissociated. Tf (solvent) is 0 C. Hence, Tf is -19.27 C. The boiling point can be obtained from the formula Tb= Tb(solvent)+ Kb* m* n where Kb is 0.512 C/m. Tb (solvent)Tb is 100 C. Tb then is 105.30 C.

Answer 2

`T_f=19.3^oC\\T_b=105.3^oC`

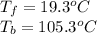
Step-by-step explanation:

Hello,

In this case, it firstly necessary to understand how the complete (100%) dissociation of the potassium phosphate is done:

`K_3PO_4(aq)\rightarrow 3K^+(aq)+PO_4^(-3)(aq)`

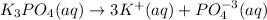
In such a way, since the freezing point depression and the boiling point elevation are computed as:

`(T_f-T_(pure))=i*m*K_f`

`(T_b-T_(pure))=i*m*K_b`

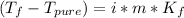
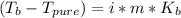
The corresponding van't Hoff factor is four as 3 potassiums and 1 phosphate as ions are obtained during the dissolution. In addition, the freezing point depression constant and boiling point elevation constant of water are 1.86 and 0.512 °C/m respectively. Moreover, the freezing point of water is 0 °C and the boiling point is 100 °C, therefore, the resulting freezing and boiling temperatures for the 2.59 m solution of potassium phosphate are:

`T_f=0^oC+4*2.59m*1.86^oC/m\\T_f=19.3^oC\\\\T_b=100^oC+4*2.59m*0.512^oC/m\\T_b=105.3^oC`

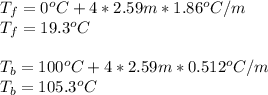
Best regards.