a) y = x - 2
b) y = -x -6
Step-by-step explanation:
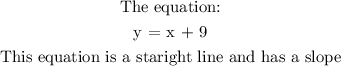
a) parallel line that passes through (-2, -4)
For a line to be parallel to another line, the slope of both lines must be equal
y = x + 9
comparing with equation of line:
y = mx + b
mx = x
m = 1
Slope of first line = 1
slope of the 2nd line = 1
For the 2nd line, it passes through (-2, -4)
x = -2, y = -4
y = mx + b
-4 = 1(-2) + b
-4 = b - 2
-4 + 2 = b - 2 + 2
-2 = b + 0
b = -2
The equation parallel to y = x + 9 becomes:
y = x + (-2)
y = x - 2
b) For a line to be perpendicular to another line, the slope of one line will be thenegative reciprocal of the other line.
slope of 1st line = 1
reciprocal of the line = 1/1 = 1
negative reciprocal = -1
point (-2, -4)
y = mx + b
-4 = -1(-2) + b
-4 = 2 + b
-4 -2 = b
b = -6
The equation perpendicular to the line y = x + 9:
y = -1(x) + (-6)
y = -x -6