Answer:
Both equation are symmetric about the x-axis.
Explanation:
If (r,θ) can be replaced by (r,-θ),then the graph is symmetric about the x-axis.
If (r,θ) can be replaced by (-r,-θ),then the graph is symmetric about the y-axis.
If (r,θ) can be replaced by (-r,θ),then the graph is symmetric about the origin.
The given equation is
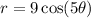
Replace the value of (r,θ) by (r,-θ).
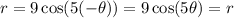
It is symmetric about the x-axis.
Replace the value of (r,θ) by (-r,-θ).
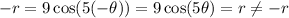
It is not symmetric about the y-axis.
Replace the value of (r,θ) by (-r,θ).
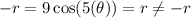
It is not symmetric about the origin.
Therefore the first equation is symmetric about the x-axis.
The given equation is
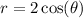
Replace the value of (r,θ) by (r,-θ).
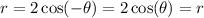
It is symmetric about the x-axis.
Replace the value of (r,θ) by (-r,-θ).
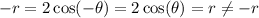
It is not symmetric about the y-axis.
Replace the value of (r,θ) by (-r,θ).
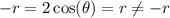
It is not symmetric about the origin.
Therefore the second equation is symmetric about the x-axis.