Answer:
Average Rate of change of d(t) is 11.43
Explanation:
Given:
d(t) = 4.9 t²
where d(t) gives distance covered by coin in time t.
To find: The Average Rate of change of d(t) from t = 3 to t = 6.
We know that Average rate of change, A of f(x) =
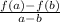
here, a= 6 and b = 3
So, Average rate of change =

=
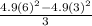
=

=
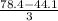
=

=
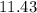
Therefore, Average Rate of change of d(t) is 11.43