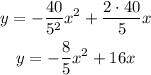Two possible real life situations are: shooting a cannon and hitting a golf ball. In both cases, variable x-variable will represent time (the time after the cannonball was shot and the time after the golf ball was hit), and the y-variable will represent the height of the cannonball and the golf ball.
In both cases, the point (0,0) is included.
Let's suppose that the maximum height reached by the golf ball is 20 ft and it takes 3 seconds to reach that height. The ball will reach the soil after another 3 seconds, making a total of 3 + 3 = 6 seconds. Therefore, the points (3, 20) and (6, 0) will be on the parabola too.
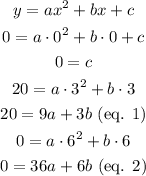
Multiplying equation 1 by 2 and subtracting equation 2 to that result, we get:
2*20 = 2(9a + 3b)
40 = 18a + 6b
40 = 18a + 6b
-
0 = 36a + 6b
------------------------
40 = -18a
40/(-18) = a
-20/9 = a
And the value of b is:
40 = 18(-20/9) + 6b
40 = -40+ 6b
40 + 40 = 6b
80/6 = b
40/3 = b
And the equation is:
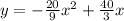
This formula has the form:
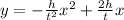
where the point (t, h) is the vertex of the parabola. So, in the case of the cannonball, let's suppose that the maximum height is 40 ft and it takes 5 seconds to reach that height. Then the equation will be: