Question

42% of adults say cashews are their favorite kind of nut. You randomly select 12 adults and ask each to name his or her favorite nut. Find the probability that the number whosay cashews are their favorite nut is (a) exactly three, (b) at least four, and (c) at most two. If convenient, use technology to find the probabilities.(a) P(3) =(Round to the nearest thousandth)

Answer 1

The formula for binomial probabilities is-

`P(x)=(n!)/((n-x)!\cdot x!)\cdot p^x\cdot q^(n-x)`

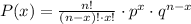
According to the problem, n = 12, p = 0.42. Since the selection is 12 adults and the percentage is 42%.

Let's find q

`q=1-p=1-0.42=0.58`

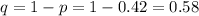
For (a) exactly three, x = 3. So, let's replace all the values in the formula.

`P(3)=(12!)/((12-3)!\cdot3!)\cdot(0.42)^3\cdot(0.58)^(12-3)`

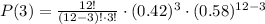
Using a calculator, we have

`P(3)\approx0.121`

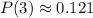
This means the probability of exactly three is 12.1%, approximately.

For (b) at least four, we have to find probability when x = 4, 5, 6, 7, 8, 9, 10, 11, 12. Using a calculator, we find each probability, then we sum.

`P(\ge4)=P(4)+P(5)+P(6)+P(7)+P(8)+P(9)+P(10)+P(11)+P(12)`
`\begin{gathered} P(4)=(12!)/(\left(12-4\right)!\cdot4!)\cdot\mleft(0.42\mright)^4\cdot\mleft(0.58\mright)^(12-4)\approx0.197 \\ P(5)=(12!)/(\left(12-5\right)!\cdot5!)\cdot\mleft(0.42\mright)^5\cdot\mleft(0.58\mright)^(12-5)\approx0.229 \\ P(6)=(12!)/(\left(12-6\right)!\cdot6!)\cdot\mleft(0.42\mright)^6\cdot\mleft(0.58\mright)^(12-6)\approx0.193 \\ P(7)=(12!)/(\left(12-7\right)!\cdot7!)\cdot\mleft(0.42\mright)^7\cdot\mleft(0.58\mright)^(12-7)\approx0.120 \\ P(8)=(12!)/(\left(12-8\right)!\cdot8!)\cdot\mleft(0.42\mright)^8\cdot\mleft(0.58\mright)^(12-8)\approx0.054 \\ P(9)=(12!)/(\left(12-9\right)!\cdot9!)\cdot\mleft(0.42\mright)^9\cdot\mleft(0.58\mright)^(12-9)\approx0.017 \\ P(10)=(12!)/(\left(12-10\right)!\cdot10!)\cdot\mleft(0.42\mright)^(10)\cdot\mleft(0.58\mright)^(12-10)\approx0.004 \\ P(11)=(12!)/(\left(12-11\right)!\cdot11!)\cdot\mleft(0.42\mright)^(11)\cdot\mleft(0.58\mright)^(12-11)\approx0.0005 \\ P(12)=(12!)/(\left(12-12\right)!\cdot12!)\cdot\mleft(0.42\mright)^(12)\cdot\mleft(0.58\mright)^(12-12)\approx0.00003 \end{gathered}`

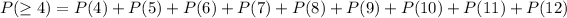
Now, we sum all.

`P(\ge4)=0.197+0.229+0.193+0.120+0.054+0.017+0.004+0.0005+0.00003=0.815`

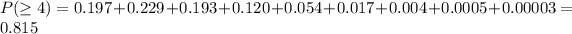
Therefore, the probability of at least four is 81.5%, approximately.

At last, for (a) at most two, the probability would be the sum of probabilities when x = 1, 2.

`\begin{gathered} P(1)=(12!)/(\left(12-1\right)!\cdot1!)\cdot\mleft(0.42\mright)^1\cdot\mleft(0.58\mright)^(12-1)\approx0.013 \\ P(2)=(12!)/(\left(12-2\right)!\cdot2!)\cdot\mleft(0.42\mright)^2\cdot\mleft(0.58\mright)^(12-2)\approx0.050 \end{gathered}`

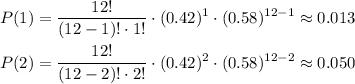
So, the sum would be

`P(\leq2)=P(1)+P(2)=0.013+0.050=0.063`

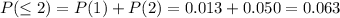
Therefore, the probability of at most two is 6.3%, approximately.