Question

The point (-3/5,y)in the third quadrant corresponds to angle θ on the unit circle.

The value of sec θ is?
The value of cot θ is ?

Answer 1

Hello,

cos(x)=-3/5

sin(x)=-√(1²-(-3/5)²=-4/5

sec(x)=1/ cos(x)=1/-(3/8)=-5/3

cot(x)= cos(x)/sin(x)=(-3/5)/(-4/5)=3/4

Answer 2

The given point (-3/5 , y) lies in the third quadrant.
It is also given that the point lies on a unit circle.

For a point (x,y) lying on a unit circle a and y are defined as:

x = cos θ
y = sin θ

So, we can say for the point (-3/5 , y) the value -3/5 is equal to cos θ

sec θ is the reciprocal of cos θ.

So, sec θ = -5/3


`cot\theta= (cos\theta)/(sin\theta)`

Using Pythagorean identity we can first find sin θ.


`sin \theta = - \sqrt{1- cos^(2)\theta } \\ \\ sin\theta= \sqrt{1-( -(3)/(5))^(2) }=- (4)/(5)`

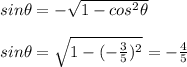
Since the point lies in 3rd quadrant, both sin and cos will be negative.

So, now we can write:


`cot\theta= ( (-3)/(5) )/( (-4)/(5) ) \\ \\ cot\theta= (3)/(4)`

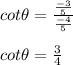Answers:
sec θ = -5/3
cot θ = 3/4