Question

Which function has an inverse that is a function?

b(x) = x2 + 3
d(x) = –9
m(x) = –7x
p(x) = |x|

Answer 1

Hello,

Answer C

y=-7x ==>x=-7y==>y=-x/7 is the inverse of m(x)
======================

Answer 2

On the attached diagram you can see all graphs of functions b(x), d(x), m(x) and p(x).

Finding the inverse of a function f(x):

1. First, replace f(x) with y. This is done to make the rest of the process easier.

2. Replace every x with a y and replace every y with an x.

3. Solve the equation from Step 2 for y. This is the step where mistakes are most often made so be careful with this step.

4. Replace y with
`f^(-1)(x).` In other words, you’ve managed to find the inverse.

5. Remember: the domain of f is the range of
`f^(-1)` and the range of f is the domain of
`f^(-1)`.

Using this algorithm, you can find the inverse only in case C:

for m(x)=-7x:

1. y=-7x.

2. x=-7y.

3. y=-x/7.

4.
`m^(-1)(x)=-(x)/(7)`.

5. The domain and the range of m(x) are all real numbers as well as the domain and the range of
`m^(-1)(x).`

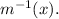
Functions b(x) and p(x) are not one-to-one functions (see attached diagram), then you can't find an inverse function. Function d(x) doesn't include x, then you can't also find an inverse function.