Question

Calculate the average rate of change for the given graph from x = –2 to x = 0 and select the correct answer below.

please and thank you

Answer 1

Average rate of change(A(x)) of f(x) over the interval [a, b] is given by:

`A(x) = (f(b)-f(a))/(b-a)`

As per the statement:

From the given graph as shown :

At x = -2

then;

f(-2) = -1

At x = 0

then;

f(0) = -1

To find the average rate of change for the given graph from x = –2 to x = 0 .

Substitute the given values we have;

`A(x) = (f(0)-f(-2))/(0+2)`

⇒
`A(x) = (-1-(-1))/(2)`

⇒
`A(x) = (-1+1)/(2)`

⇒
`A(x) =0`

Therefore, the average rate of change for the given graph from x = –2 to x = 0 is, 0

Answer 2

Keywords:

average rate of change, parabola, interval, points

For this case we have to find the average rate of change of a parabola in the interval from
`x = -2` to
`x = 0`. To do this, we need two points for the parabola pass, and apply the following formula:

`AVR = \frac {f (x_ {2}) - f (x_ {1})} {x_ {2} -x_ {1}}`

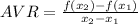
We have the following points, taking into account that
`y = f (x)`:

`(x_ {1}, f (x_ {1})) = (- 2, -1)\\(x_ {2}, f (x_ {2})) = (0, -1)`

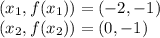
Substituting:

`AVR = \frac {-1 - (- 1)} {0 - (- 2)}\\AVR = \frac {-1 + 1} {0 + 2}\\AVR = 0`

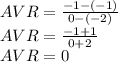
So, the average rate of change for the given graph is 0 in the given interval

Answer:

`AVR = 0\ from\ x = -2\ to\ x = 0`