ANSWER

Step-by-step explanation
We want to factor

Observe that, both

and
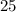
are perfect squares.
Thus,

and

We need to rewrite the expression as a difference of two squares to obtain,

We apply the difference of two squares formula which is given by,

By comparing this to our expression we let

Then our expression can now be factored as,

Therefore the correct option is B.