Question

Andy completes the square for the equation x2 + 6x - 8 = 0. Which of the following equations reveals the vertex of the parabola? will fan and medal

Answer 1

(h,k) in the cuadratic formula y= a(x-h)^2 + k

Explanation:

If you complete square in a cuadratic formula the vertex of the parabola will be more visible. In the case of f(x)=
`x^(2)+6x-8` we complete square adding and substracting 9. So,

`x^(2)+6x+9-9-8 = (x+3)^(2)-17`

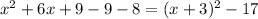
So we have the cuadratic form of a parabola
`y= a(x-h)^(2) + k` where a=1, h= -3 and k= -17.

So, the vertex is (h,k)=(-3,-17).

Answer 2

If the equation
`x^2+6x-8` has undergo completing the square, the answer would be:

`x^2+6x-8`

`x^2+6x+9-8-9`
**In this example, since 6x is the middle term, what comes to my mind is the polynomial (x+3) because 2ab results into 6x. [from the special products lesson
`(a+b)^2=a^2+2ab+b^2` ]

`(x+3)^2 -17 = 0`
So if the equation is equal to y, then this equation's

`y+17=(x+3)^2`
The vertex would be on the point (-3, -17)