Question

Determine if the graph is symmetric about the x-axis, the y-axis, or the origin.
r = 9 sin 7θ

Answer 1

The given function symmetric about the y-axis.

Explanation:

The given function is

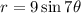`r=9\sin 7\theta` .... (1)

1. Symmetry about the x-axis: If the point (r, θ ) lies on the graph, then the point (r,-θ ) or (-r, π - θ ) also lies on the graph.

2. Symmetry about the y-axis: If the point (r, θ ) lies on the graph, then the point (r,π - θ ) or (-r, -θ ) also lies on the graph.

3. Symmetry about the origin: If the point (r, θ ) lies on the graph, then the point (-r, θ ) or (r, π + θ ) also lies on the graph.

Put (r, -θ ) in the given function.

`r=9\sin 7(-\theta)=-9\sin 7\theta=-r\\eq r`

Therefore it is not symmetric about x-axis.

Put (-r, -θ ) in the given function.

`-r=9\sin 7(-\theta)=-9\sin 7\theta=-r`

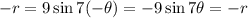
Therefore it is symmetric about y-axis.

Put (-r,θ ) in the given function.

`-r=9\sin 7(\theta)=r\\eq -r`

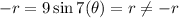
Therefore it is not symmetric about the origin.