Answer:
The length is 38 units and the width is 12 units.
Explanation:
We have to express the problem in equations.
 is gonna be length,
is gonna be length,
 is gonna be width and
is gonna be width and
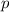 is the perimeter.
is the perimeter.
The length is 2 more than 3 times the width is

The perimeter is 100 refers to

Now, we know that the perimeter of a rectangle is expressed

Replacing the first expression in the second equation, we have:

Now, we replace this value in the first expression to find the length:

Therefore, the length is 38 units and the width is 12 units.