Question

Functions 1 and 2 are shown below:

Function 1: f(x) = −3x2 + 2
A graph of a parabola with x intercepts of negative 0.5, 0 and 2, 0 and a vertex of 0.5, 4 is shown.

Which function has a larger maximum? Type your answer as 1 or 2.

Answer 1

the anwser is 2 guys. i got it correct

Answer 2

The function 2 has a larger maximum.

Explanation:

The vertex form of the parabola is

`f(x)=a(x-h)^2+k` .... (1)

Where, (h,k) is the vertex.

The given functions are

`f(x)=-3x^2+2` ..... (2)

Since the leading coefficient is negative, therefore it is a downward parabola. It means the vertex of the parabola is the maximum point.

On comparing (1) and (2), we get

`h=0,k=2`

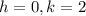
Therefore the maximum value of the function is 2 at x=0.

The second function has x intercepts of (-0.5, 0) and (2, 0) and a vertex of (0.5, 4).

It is also a downward parabola because the parabola has two x-intercepts and the vertex lies above the x-axis.

Since the vertex is (0.5, 4), therefore the maximum value of the function is 4 at x=0.5.

`Maximum(F_1)=2`

`Maximum(F_2)=4`

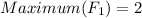
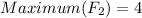
Therefore function 2 has a larger maximum.