Question

On discovering that her family had a 70% risk of heart attack, Erin took a treadmill test to check her own potential of having a heart attack. The doctors told her that the reliability of the stress test is 67%. The test predicted that Erin will not have a heart attack. What is the probability after the test was taken that she will have a heart attack?

A. 0.4051

B. 0.5010

C. 0.4653

D. 0.6632

Answer 1

The probability that she will not have a heart attack and the test predicts that she will is 0.4653 or 46.53%

Explanation:

Hint- This a conditional probability problem where Bayes theorem should be applied.

Applying Bayes theorem,

`P(\text{No heart attack}\ |\ \text{Correctly tested})=`

`\frac{P(\text{Correctly tested}\ |\ \text{No heart attack})\cdot P(\text{No heart attack})}{P(\text{Correctly tested})}`

`P(\text{Correctly\ tested}\ |\ \text{No\ heart\ attack})=67\%=0.67`

`P(\text{No\ heart\ attack})=1-P(\text{heart\ attack})=1-0.7=0.3`

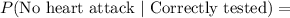
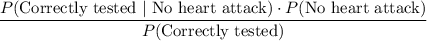
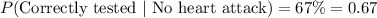
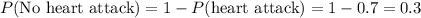
`P(\text{Correctly\ tested})=[P(\text{No\ heart\ attack})* P(\text{Correctly\ tested})]+[P(\text{Heart\ attack})* (\text{Incorrectly\ tested})]`

`=[0.3* 0.67]+[0.7* 0.33]=0.432`

Putting the values,

`P(\text{No\ heart\ attack}\ |\ \text{Correctly\ tested})=(0.67* 0.3)/(0.432) =0.4653`

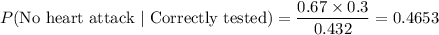
∴ There is a probability of 0.4653 or 46.53% chance that she will not have a heart attack even though the test predicts that she will.