Axis of symmetry is a line passing through the vertex which divides the curge into two parts such tha each part looks the same.
For
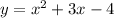
, the 'x' part is squared and the coefficient of

is positive. Hence, the curve will be a parabola facing up which means that the axis of symmetry will be a vertical line. i.e. x = m.
Investigating, f(-1) =

f(-1.5) =
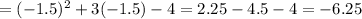
f(-2) =
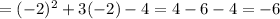
From these, the curve has a vertex at point (-1.5, -6)
Therefore the axis of symmetry is line x = -1.5 (i.e. the third option)