Answer: The correct option is (B) negative square root 21 over 5.
Step-by-step explanation: Given that for an angle
 ,
,
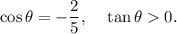
We are to find the value of
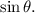
We know that
Cosine is negative in Quadrant II and Quadrant III.
Tangent is positive in Quadrant 1 and Quadrant III.
So, the given angle
 lies in the Quadrant III.
lies in the Quadrant III.
We will be using the following trigonometric identity:
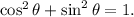
We have
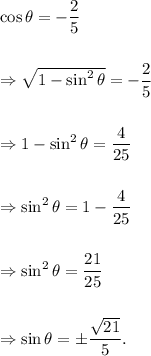
Since the angle
 lies in Quadrant III and sine is negative in that quadrant, so
lies in Quadrant III and sine is negative in that quadrant, so

Thus, option (B) is correct.